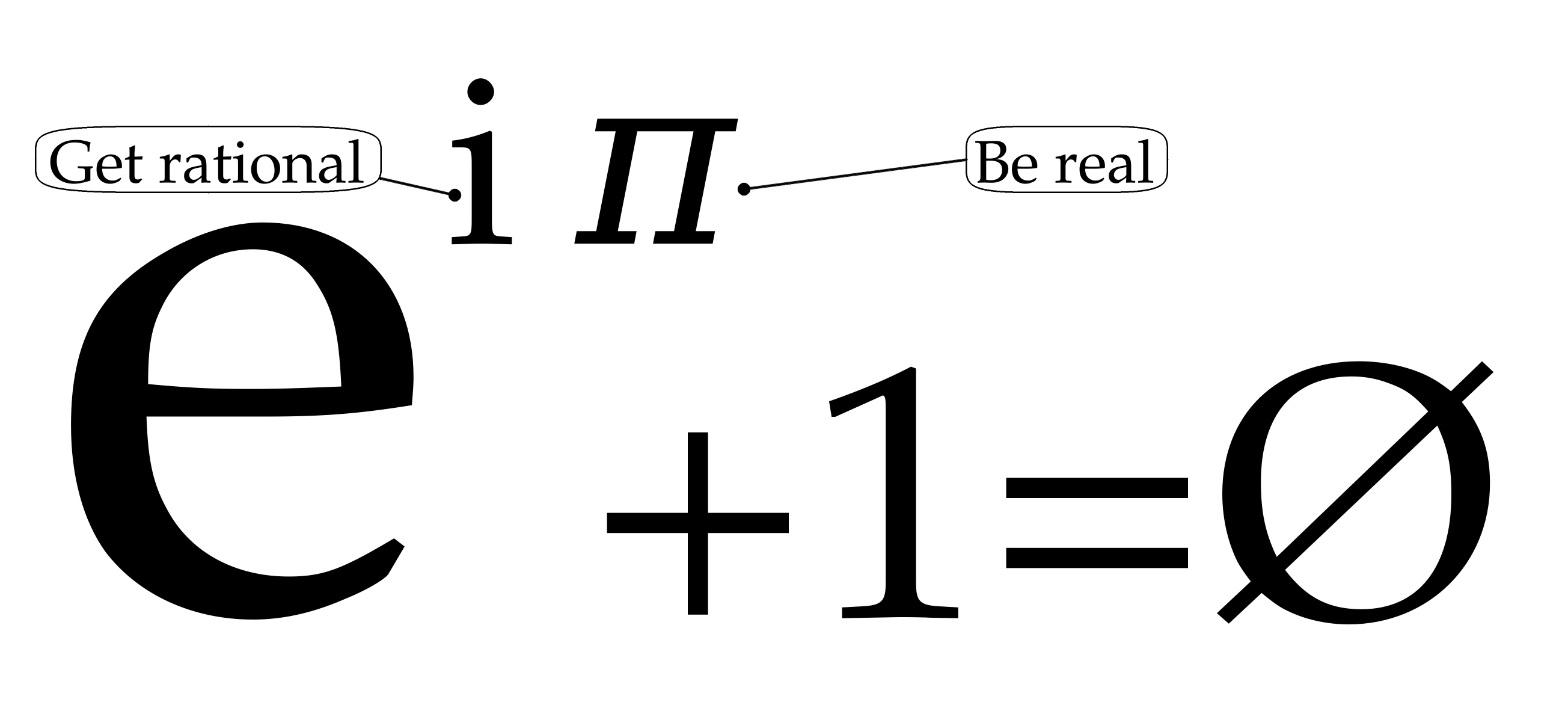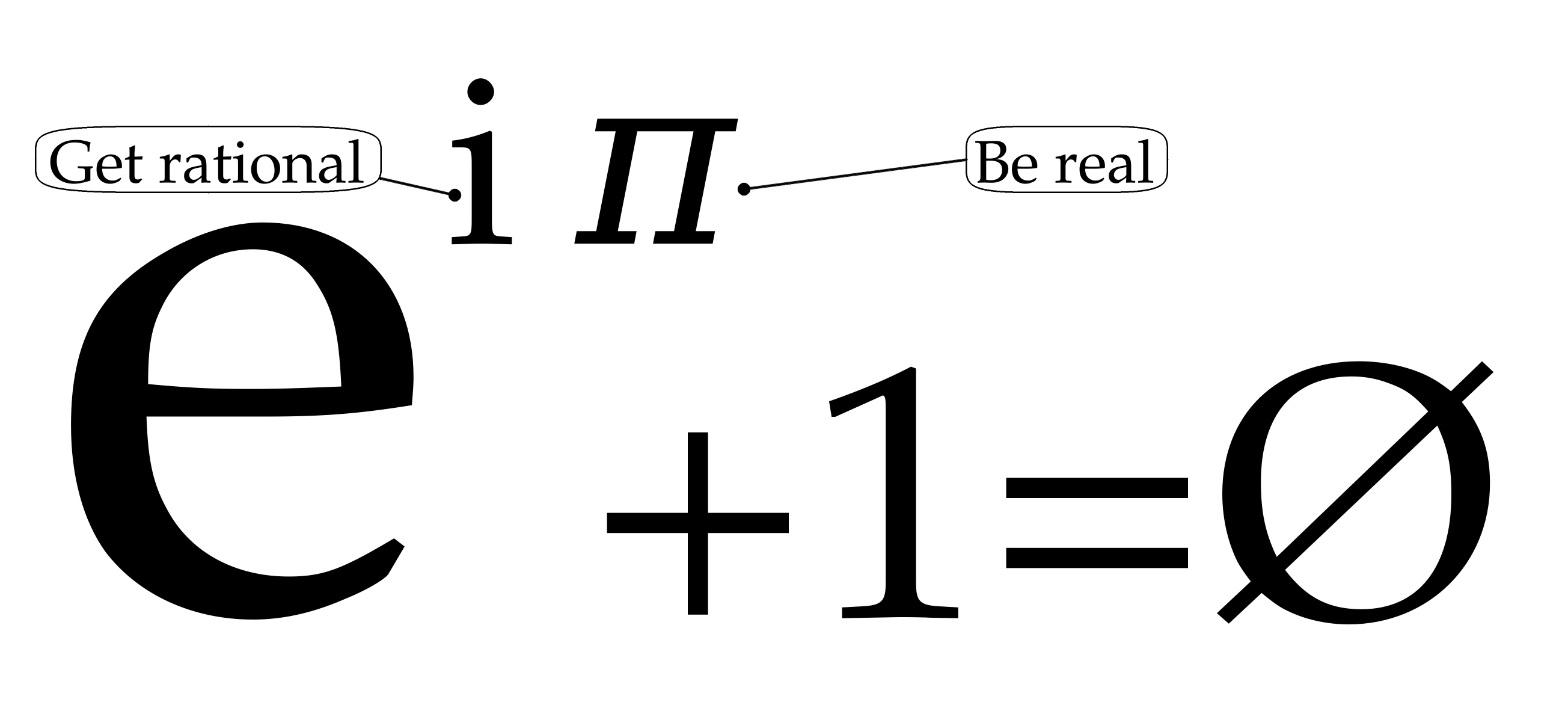De Euler-formule

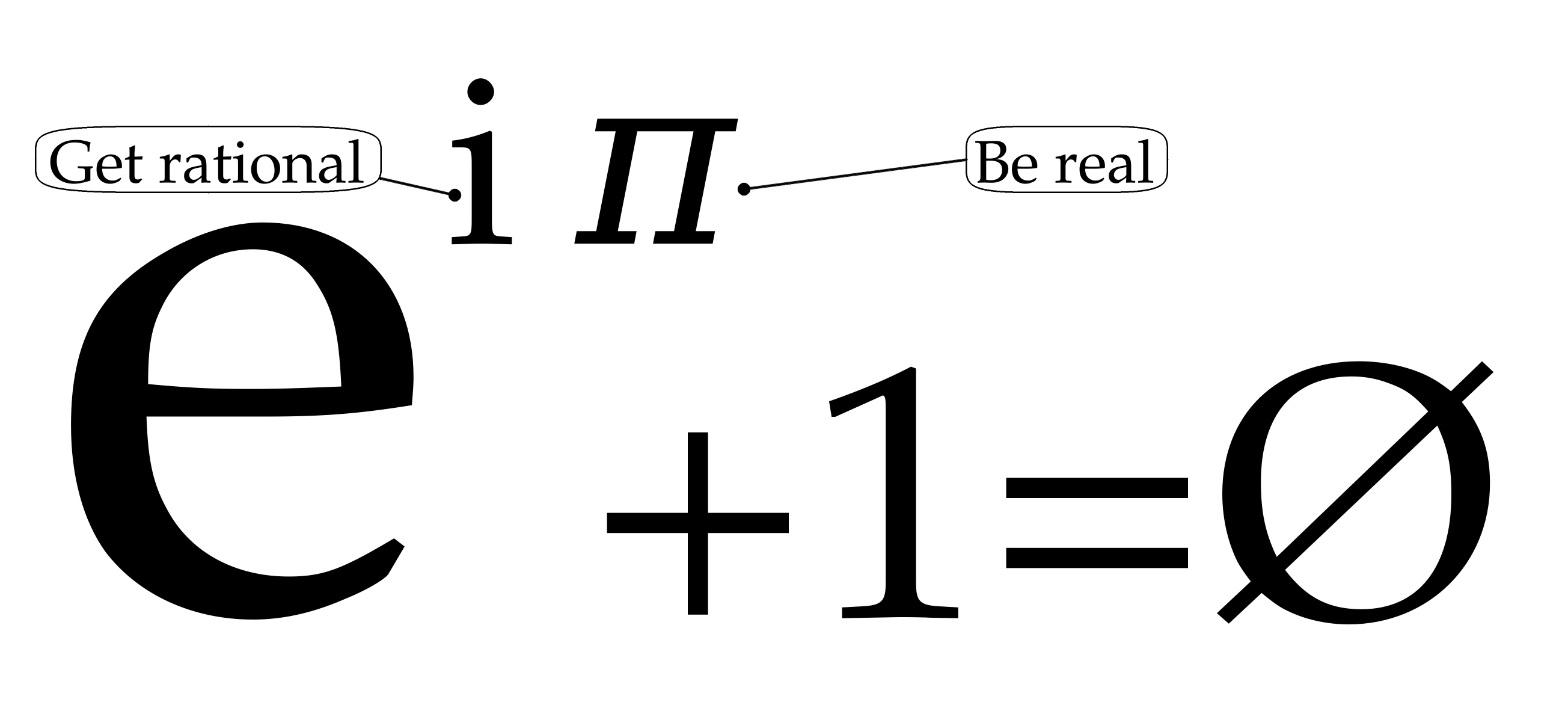
http://www.sciencecafeovervecht.nl/SBM2016/T-shirt.jpg

Wiskundige achtergrond

Bovenstaande vergelijking is geformuleerd door de Zwitserse wiskundige Leonard Euler (1707-1782). De symbolen betekenen het volgende:

• π (pi, de verhouding tussen de omtrek en diameter van een cirkel) 3.14159265358979323846...
• e (Euler's constante) 2.7182818284590452354...
Het bezondere van Euler's constante is dat ∂e^x/∂x=e^x .
• i = √-1 (een imaginair getal).
π en e zijn irrationele getallen die niet als een breuk geschreven kunnen worden. (Dat is bewijsbaar).

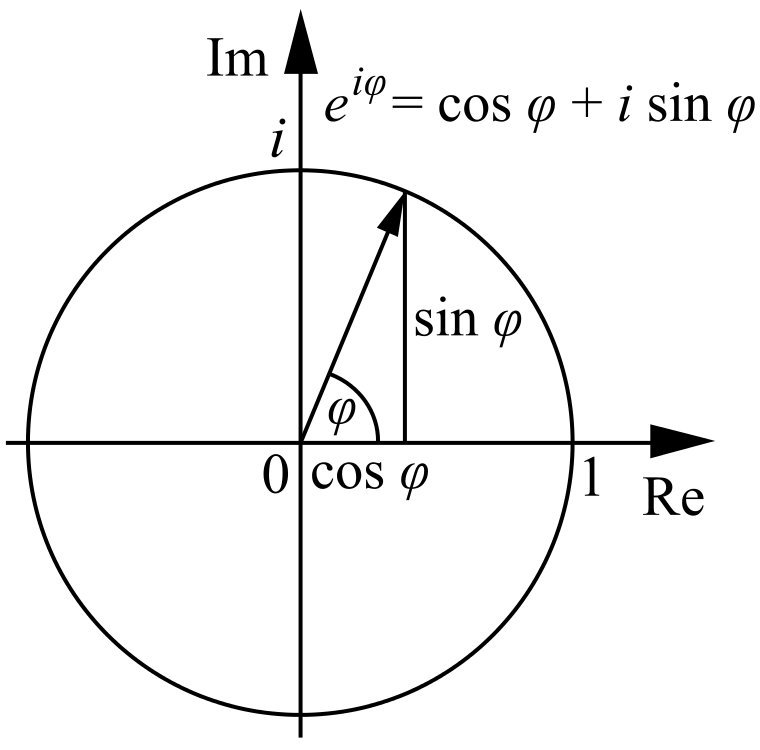
Euler's vergelijking is een bijzonder geval van e^iφ = cos(φ) + i*sin(φ)
Dat is in te zien als je weet (of kunt afleiden door te differeniëren) dat
e^x=1+(x)+(x*x/2)+(x*x*x/2*3)+(x*x*x*x/2*3*4)+(x*x*x*x*x/2*3*4*5)+...
cos(x)=1-(x*x/2)+(x*x*x*x/2*3*4)-(x*x*x*x*x*x/2*3*4*5*6)+...
sin(x)=x-(x*x*x/2*3)+(x*x*x*x*x/2*3*4*5)-(x*x*x*x*x*x*x/2*3*4*5*6*7)+...
en bedenkt dat i*i= -1.

Grafisch ziet het er zo uit met rechts een portret van Euler uit 1753:

http://www.sciencecafeovervecht.nl/SBM2016/760px-Euler.s_formula.jpg

http://www.sciencecafeovervecht.nl/SBM2016/Leonhard_Euler.jpg

Wikipedia pagina's
Nederlands
Engels
(Grafische illustratie ontleend aan Wikipedia.)